Definizione

Curve piane generate dall’intersezione di un cono circolare retto con un piano generico. Analiticamente sono la rappresentazione grafica delle funzioni algebriche di secondo grado. Sono di grande importanza per la loro significativa genesi geometrica e per le innumerevoli applicazioni in architettura.

Generalità

Fondamentalmente sono di tre tipi, definibili geometricamente in funzione della posizione del piano che interseca il cono e analiticamente in funzione del loro comportamento nei confronti della retta impropria del piano, vale a dire in relazione al numero di punti impropri che possiedono.

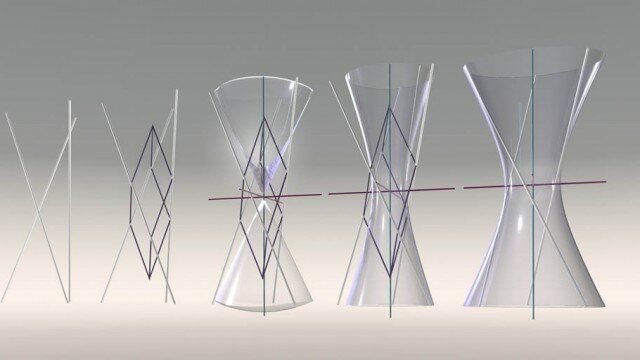
1. Le ellissi sono la famiglia di coniche per le quali il piano secante taglia una sola falda del cono; analiticamente sono prive di punti impropri (reali). La loro forma può variare in funzione della dimensione e dello schiacciamento, vale a dire dell’eccentricità. Alla famiglia delle ellissi appartengono anche le circonferenze che ne costituiscono casi particolari (piano secante ortogonale all’asse del cono).
2. Le circonferenze hanno eccentricità nulla e differiscono tra loro solo per la dimensione. Le iperboli sono la famiglia di coniche per le quali il piano secante taglia due falde del cono; analiticamente hanno due punti impropri. Sono caratterizzate dagli asintoti, rette tangenti nei punti impropri. La loro forma, come le ellissi, può variare in funzione della dimensione e dello schiacciamento, vale a dire dell’angolo formato dagli asintoti. Particolari sono le iperboli equilatere i cui asintoti sono ortogonali; le iperboli equilatere differiscono tra loro solo per la dimensione.
3. Le parabole sono la famiglia di coniche per le quali il piano secante è parallelo ad una generatrice del cono; analiticamente hanno un solo punto improprio (due punti coincidenti), nel quale sono tangenti alla retta impropria. La loro forma può variare solo nella dimensione: tutte le parabole infatti sono simili, come le circonferenze.

Le tre famiglie di coniche sono contigue, nel senso che sono trasformabili l’una nell’altra con continuità, senza interruzioni, come la loro genesi proiettiva chiarisce. Le parabole costituiscono la famiglia di transizione tra le ellissi e le iperboli e possono considerarsi come la loro condizione limite. Le ellissi e le iperboli hanno due assi di simmetria, le parabole ne hanno uno solo. Sono coniche degeneri quelle per le quali il piano secante passa per il vertice del cono; a seconda della sua giacitura l’intersezione sarà un punto oppure si spezzerà in due rette distinte o in due rette coincidenti, esito rispettivamente della degenerazione delle ellissi, delle iperboli e delle parabole.
In architettura sono coniche molte curve generate dall’intersezione di superfici quadriche, vale a dire coni, cilindri, sfere, paraboloidi, ellissoidi e iperboloidi (posti in condizioni particolari) tra loro o con piani. Nella rappresentazione le coniche vengono incontrate di frequente come deformate proiettive delle circonferenze e nella costruzione delle ombre generate dalle intersezioni di fasci di luce cilindrici o conici con superfici piane, o anche di piani di luce con superfici cilindriche o coniche.
Una teoria sulla loro genesi e sulle loro proprietà geometriche e matematiche fu sviluppata organicamente già alla fine del II secolo a.C. per opera di Apollonio di Perga che ne comprese e approfondì la genesi proiettiva. La sua opera fu poi ripresa e completata da Pappo di Alessandria agli inizi del III secolo, per poi restare sostanzialmente senza importanti sviluppi fino alla fine del XIV secolo, quando Federico Comandino tradusse e pubblicò (1588) l’opera di Apollonio e di Pappo, con ampliamenti e integrazioni.
Seguirono gli studi di molti matematici che giunsero alla formulazione completa della teoria generale delle coniche; tra questi Girard Desargues (metà del XV secolo) e Pierre Dandelin (primi decenni del XVII secolo) che ne estesero notevolmente sia l’ambito teorico che le applicazioni allo spazio tridimensionale. Oggi Riccardo Migliari ne prosegue e amplia lo studio con l’uso dell’informatica rendendo accessibili anche costruzioni e rappresentazioni di morfologie complesse, prima impensabili con le procedure grafiche tradizionali.

 

Copyright © - Riproduzione riservata