Definizione – Etimologia
La geometria descrittiva è la scienza che studia il modo di rappresentare visivamente le forme a tre dimensioni e studia altresì le loro proprietà geometriche per mezzo di tale rappresentazione. L’espressione geometria descrittiva allude da un lato alla possibilità di misurare le forme suddette (geometria, dal greco γεωμετρία, atto del misurare la terra), dall’altro alla necessità di descriverle per mezzo di immagini (descrittiva, dal latino descríbĕre, descrivere).
Storia
Il termine Géométrie Descriptive fu coniato da Gaspard Monge, alla fine del 1794, per designare un insieme di teorie e procedure grafiche in uso presso il genio militare, da lui codificate nel quadro di una nuova scienza. Queste procedure consistevano, essenzialmente, nell’associare due proiezioni parallele dell’oggetto da rappresentare (la pianta e l’alzato) assumendo i due disegni come piani di riferimento e considerando le intersezioni di rette e piani dello spazio tridimensionale (detti tracce) con i suddetti piani. Così facendo, rappresentazioni tecniche note da secoli potevano proporsi come efficace strumento per la soluzione di problemi progettuali complessi.
Esempi di questi problemi, tipici delle strategie militari dell’epoca, sono il defilamento, ovvero la protezione delle piazzeforti dai tiri dell’artiglieria, o, ancora, la determinazione della posizione nello spazio di un pallone frenato, noti i tre angoli formati dai raggi di collimazione, da uno strumento posto sul pallone, di tre punti noti a terra (problema del vertice di piramide).
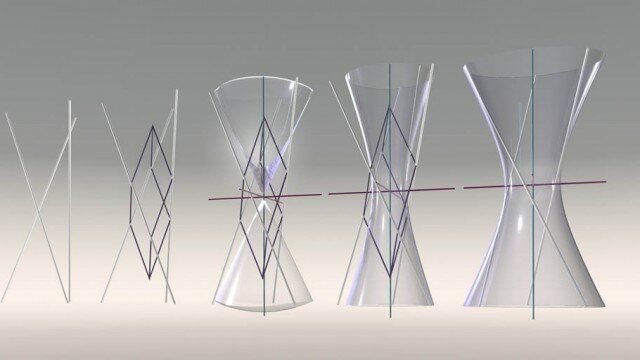
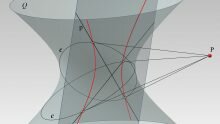
Il metodo di Monge si prestava anche alla rappresentazione delle superfici di secondo grado e perciò allo studio sintetico, cioè grafico e non simbolico, delle loro proprietà, nonché alla soluzione di altri problemi squisitamente geometrici come quelli di posizione.
Alla questione del contributo di Monge alla scienza che da lui ha avuto il nome, si danno risposte contrastanti: secondo alcuni egli sarebbe il creatore della geometria descrittiva, secondo altri egli avrebbe solo autorevolmente contribuito a una Storia che ha origini nell’antichità e prosegue ancora ai giorni d’oggi. Ad esempio, le costruzioni grafiche utilizzate da Piero della Francesca nel suo trattato De prospectiva pingendi (scritto tra il 1482 e il 1492), sono a tutti gli effetti proiezioni ortogonali associate come quelle di Monge e, risalendo anche più indietro nel tempo, anche la icnografia e la ortografia vitruviane (I sec.) sono disegni di questo tipo. Inoltre, se si considerano i più recenti strumenti digitali della progettazione architettonica, è possibile ritrovare negli algoritmi e nelle procedure impiegate, ancora teorie e metodi che appartengono in tutto alla geometria descrittiva, perché sono una generalizzazione delle teorie e dei metodi storicizzati.
Ruolo della geometria descrittiva nella scienza e nella tecnica
La geometria descrittiva, già nel tempo della sua prima codificazione teorica, svolge un duplice ruolo: da un lato rappresenta un importante perfezionamento degli strumenti grafici impiegati nel progetto di architettura e di ingegneria, dall’altro integra, con l’immagine e con le logiche tipiche della geometria sintetica, i linguaggi simbolici della geometria analitica e differenziale. A questi due ruoli corrispondono, nell’ottocento, due linee di sviluppo: la prima prevalentemente applicativa, la seconda prevalentemente teorica. Tipici sviluppi applicativi sono quelli che riguardano le arti, tra le quali anche l’architettura, come il disegno degli ordini e la resa del chiaroscuro. I più importanti sviluppi teorici sono invece quelli che riguardano le proprietà delle superfici rigate e delle rigate sviluppabili e la geometria proiettiva.
Struttura della disciplina prima della rivoluzione informatica
La disciplina si è così evoluta fino alla prima metà del Novecento, quando ha consolidato i suoi contenuti in un sistema articolato in tre parti: i metodi, lo studio delle figure geometriche dello spazio, le applicazioni.
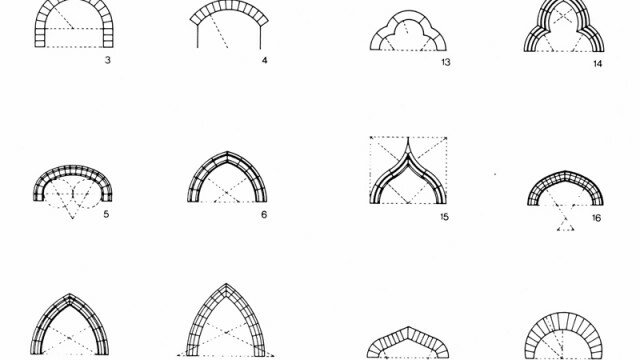
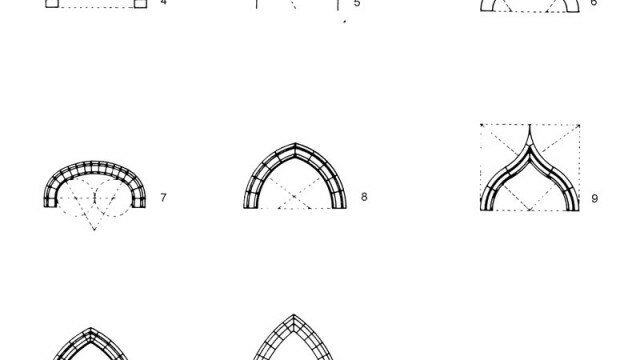
I metodi che costituiscono il corpus disciplinare alla metà del novecento sono: la doppia proiezione ortogonale o metodo di Monge, l’assonometria, la proiezione quotata, la proiezione centrale. Lo studio delle superfici riguarda, essenzialmente, i poliedri e le superfici di secondo grado, con qualche accenno a superfici algebriche di ordine superiore al secondo, come il toro e le ciclidi. La terza parte riguarda le applicazioni, che spaziano dalla prospettiva, intesa come immagine e non come metodo autonomo, alla resa degli effetti della luce sui corpi, alla costruzione delle volte, alla stereotomia della pietra e del legno, al progetto degli ingranaggi.
Si perviene così a definire la distinzione tra metodo di rappresentazione e strumento applicativo, che è di fondamentale importanza nell’assetto attuale della disciplina. Ha dignità di metodo quell’insieme di teorie e di procedimenti che consente di rappresentare un oggetto tridimensionale, di operare su di esso come si farebbe sopra un modello fisico e di ricostruire l’oggetto rappresentato nello spazio. Il metodo è tale quando è capace di tutto ciò in completa autonomia e senza l’intervento di altri metodi. Strumento è invece quel sistema che, grazie alla applicazione di uno o più metodi, porta al conseguimento di un risultato efficace nell’ambito dell’attività progettuale o esecutiva. Questa distinzione è fondamentale perché permette, come vedremo, di distinguere due nuovi metodi della geometria descrittiva, dalle applicazioni che ne fanno uso, che sono gli attuali programmi informatici per la modellazione digitale a tre dimensioni.
Modus operandi della geometria descrittiva
Per comprendere appieno il significato della geometria descrittiva nell’ambito del progetto di architettura, occorre ora descrivere il suo modus operandi. Così come nella geometria euclidea il ragionamento astratto, che rispetta le regole del sistema logico-deduttivo, trova nel disegno delle figure piane una verifica sperimentale e la costruzione grafica, a sua volta, dimostra di per sé l’esistenza delle figure; così, nella geometria descrittiva, la ragione che costruisce forme nello spazio trova, nella rappresentazione, la verifica della loro esistenza e, al tempo stesso, le sperimenta, subendo la suggestione di nuove idee. In modo assai semplice e chiaro lo stesso Monge descrive questo effetto euristico, quando descrive i due scopi primari della disciplina: “il primo è rappresentare con esattezza, su un disegno che ha due dimensioni, gli oggetti che ne hanno tre, e che sono suscettibili di una definizione rigorosa […] il secondo … è dedurre, dalla descrizione esatta dei corpi, tutto ciò che segue necessariamente dalle loro forme e posizioni reciproche. In questo senso, è un mezzo di ricerca della verità; essa offre continui esempi del passaggio dal noto all’ignoto”.
Dunque, mentre per un verso il disegno svela l’immagine di forme solo intuite nella mente del progettista, per l’altro, proprio perché rimuove quel velo, mostra proprietà ignote e problemi inaspettati. Tale è anche, e senza alcuna distinzione, il carattere della ricerca scientifica pura, quando la semplice visualizzazione di una figura ideata in astratto, come il prodotto di movimenti e intersezioni, suggerisce risultati che si era ben lungi dall’immaginare. E non è un caso se il verbo costruire ha il medesimo uso nell’ambito della geometria astratta e nell’ambito del cantiere; al punto che la geometria descrittiva si può intendere, semplicemente, come un esercizio astratto dell’arte di progettare.
Le operazioni che il progettista esegue per mezzo della geometria descrittiva appartengono a tre tipi: la visualizzazione delle forme che ha immaginato, la misura delle stesse e la loro costruzione. Queste tre attività non si susseguono in un ordine prestabilito ma si alternano in un processo iterativo, che converge verso la definizione compiuta dell’idea progettuale.
Per quasi tutto il Novecento, gli strumenti grafici impiegati nello svolgimento delle suddette operazioni sono stati la riga e il compasso (come per la geometria classica) e, al più, alcuni ausili tecnici come il tecnigrafo. Nei primi anni Ottanta, con la diffusione dei primi personal computer, e dei primi plotter, l’accuratezza del disegno di progetto è decisamente migliorata, ma la geometria descrittiva ha continuato a svolgere i ruoli che la storia le aveva assegnato. Alla fine degli anni Ottanta, però, sono comparsi i primi elaboratori elettronici personali capaci di prestazioni tridimensionali e, da qualche anno ormai, queste prestazioni hanno raggiunto una perfezione prima inimmaginabile, tale che oggi è possibile costruire una forma a tre dimensioni modellandola in uno spazio virtuale interattivo e ricavare da questa forma i relativi disegni tecnici (piante, alzati, sezioni etc.) in modo automatico.
Struttura della disciplina dopo la rivoluzione informatica
Bisogna, dunque, prendere atto del fatto che la geometria descrittiva ha subito una trasformazione epocale: il primo dei suoi compiti storici, la visualizzazione, è oggi assolto egregiamente dalle macchine; resta invece, con tutta la sua rilevanza, il secondo degli scopi: quello che è connesso con la parte più creativa dell’attività progettuale, e cioè la costruzione delle forme ideate e la verifica che disvela i caratteri nascosti, ignoti, dell’idea.
Nello svolgimento di questo secondo compito, la geometria descrittiva è oggi assistita dalle macchine digitali molto meglio di quanto non sia stata assistita, in passato, dalla riga e dal compasso. Infatti: l’accuratezza del disegno tecnico è passata dal decimo al millesimo di millimetro; la suddetta accuratezza è ulteriormente incrementata dal fatto di poter disporre gli enti geometrici rappresentati direttamente nello spazio, senza la mediazione delle proiezioni; la costruzione si avvale non solo della retta e del cerchio, ma di qualsiasi altra linea, dato che l’accuratezza del tracciamento è la medesima; la costruzione si avvale non solo delle linee piane ma, nello spazio, anche delle superfici.
Le macchine digitali hanno anche esteso il carattere della ripetibilità. Mentre all’epoca di Monge si potevano considerare ripetibili, e perciò rappresentabili nel senso proprio del termine, solo le forme ‘suscettibili di una definizione rigorosa’, oggi sono ripetibili anche forme libere, come sono, ad esempio, le carrozzerie delle automobili, gli scafi e le complesse superfici curve dell’architettura contemporanea. Ciò si deve alla matematica delle equazioni NURBS (Non Uniform Rational B-spline), capace di rappresentare con esattezza quelle forme libere, irrazionali, che un tempo erano classificate come linee e superfici grafiche.
Infine, la sinergia tra la geometria della rappresentazione visiva e la geometria simbolica, consente oggi l’uso di strumenti che erano prima estranei al mondo della progettazione. Un esempio tra tutti è l’impiego del chiaroscuro (e delle linee isòfote, in particolare) nel controllo della continuità tra superfici. Questa applicazione è comune nella progettazione di componenti stampate dall’aspetto lucido, come quelle di plastica, vetro o metallo.
Alla luce di questi avvenimenti e delle considerazioni che ne sono scaturite, è stato recentemente proposto un nuovo assetto della geometria descrittiva, intesa come scienza che fornisce il fondamento teorico e gli strumenti operativi al disegno di progetto in tutte le sue declinazioni, siano esse grafiche tradizionali o digitali e innovative.
Ai metodi di rappresentazione classici, che restano il presidio del disegno manuale, si sono aggiunti i due metodi della rappresentazione matematica e della rappresentazione numerica o poligonale, che si trovano applicati nei principali programmi per il CAD (Computer Aided Design).
Il primo di questi metodi descrive le forme per mezzo di equazioni e può limitarsi alla rappresentazione delle superfici o estendersi alla rappresentazioni dei volumi, distinguendo il pieno dal vuoto (modellazione solida). Il secondo descrive invece le forme per mezzo di liste, che raccolgono le coordinate dei vertici di un poliedro, che approssima le forme stesse, e altre semplici informazioni, che riguardano la connessione dei suddetti vertici per mezzo di spigoli e facce. La differenza tra questi due metodi è la stessa che, nella geometria descrittiva classica, distingue il tracciamento continuo di una figura, dalla costruzione per punti della medesima e cioè: nella rappresentazione matematica la descrizione delle linee e delle superfici è continua, esatta in ogni punto, mentre nella rappresentazione numerica o poligonale la descrizione delle linee e delle superfici è discreta, esatta solo in alcuni punti caratteristici. Perciò, il primo metodo si presta alle costruzioni canoniche della geometria, come le intersezioni; mentre il secondo metodo si presta a costruzioni meno accurate ma più agili, come è ad esempio, la resa del chiaroscuro. In analogia a quanto accade con i metodi classici, anche i nuovi metodi hanno impieghi diversi nel progetto di architettura, secondo la vocazione di ciascuno di essi. La rappresentazione matematica, come la rappresentazione in pianta e alzato, è atta a esercitare un completo e accurato controllo metrico della forma, mentre la rappresentazione numerica, come la prospettiva, è adatta a esercitare il controllo percettivo dello spazio progettato.
Il riassetto della disciplina comprende poi l’adozione di nuovi strumenti per l’indagine e la costruzione geometrica; questi strumenti derivano dalla possibilità di utilizzare il calcolo digitale agendo, però, sui suoi effetti sintetici, cioè direttamente sulla forma. Ciò significa, ad esempio, utilizzare nella costruzione geometrica le coniche e le quadriche, e non solo la retta e il cerchio, ma anche punti notevoli come il baricentro (non solo delle figure piane, ma dei solidi) avendo così accesso a soluzioni generali che, in passato, erano confinate nel campo delle speculazioni teoriche. In questo senso, la nuova geometria descrittiva non fa che realizzare un auspicio dello stesso Monge, quando immaginava le potenzialità di una scienza capace di unire l’esattezza dell’analisi alla immediatezza visiva della geometria di sintesi.
Bibliografia
Fasolo O., Fondamenti geometrici della rappresentazione progettuale e tecnica dell’architettura, Roma 1980; Migliari R., Geometria descrittiva, Torino, 2009; Migliari R., Geometria dei modelli, Roma, 2003;
Saccardi U., Elementi di Proiettiva – Applicazioni della Geometria Descrittiva, Firenze 2004.