Definizione – Etimologia

Dal latino proicere (gettare innanzi, protendere), proiettiva è la branca della geometria dedicata allo studio delle proprietà che permangono invarianti per il gruppo delle trasformazioni proiettive. Essa studia le relazioni grafiche e metriche connesse alle operazioni di proiezione e sezione possibili nello spazio proiettivo e nella relativa rappresentazione sul piano. La geometria proiettiva fornisce altresì i fondamenti teorici alla geometria descrittiva, storicamente precedente e finalizzata alla descrizione dei concreti contesti fisici. Nel merito, H.S.M. Coxeter ebbe a definire la geometria descrittiva come “accidente” della geometria proiettiva. Peculiare della geometria proiettiva è il carattere “sintetico”, potendosi dimostrazioni e costruzioni eseguire per via grafica.

Struttura dello spazio proiettivo

Sono elementi fondamentali della geometria proiettiva il punto, la retta, il piano, intesi sia nella versione ordinaria (al finito) che impropria (all’infinito). Essi costituiscono lo spazio proiettivo, infinitamente esteso, quale ampliament dello spazio euclideo.
Le forme geometriche fondamentali si ottengono generando scambievolmente ciascun elemento fondamentale mediante uno o più elementi fondamentali di tipo diverso. A seconda che siano originate dal moto singolo, doppio, triplo, degli enti generatori si definiscono di prima specie (punteggiata, fascio di piani, fascio di raggi), di seconda specie (piano punteggiato, piano rigato, stella di raggi, stella di piani), di terza specie (spazio punteggiato, spazio di piani), analiticamente individuate da una, due, tre coordinate. Ogni forma ne include infinite di grado inferiore.
Gli assiomi e le proposizioni, assumendo gli elementi impropri generalizzano la collinearità, l‘incidenza, le relazioni metriche. Nello spazio proiettivo la retta è normalmente costituita da punti propri e da un punto improprio, tra loro collineari, e rette e/o piani paralleli risultano incidenti secondo i relativi elementi impropri, conservandosi il birapporto, di cui si dirà più avanti.

Operazioni fondamentali

Sono operazioni fondamentali della geometria proiettiva la proiezione e la sezione. La prima si esegue conducendo una linea (proiettante) per un punto (centro); la seconda intersecando una linea (raggio) con un’altra (asse). Trasformazioni proiettive sono quelle basate su combinazioni di proiezioni e sezioni. Nel piano iconico si dice immagine “di” un punto dello spazio (punto obiettivo) “sul” piano “da” un centro assegnato, l’intersezione (punto immagine) fra il piano e la retta proiettante condotta per centro e punto dati.

Dualità

È una proprietà profonda, generativa di questa geometria, legata alla definizione scambievole degli elementi fondamentali e alle stesse operazioni fondative di proiezione e sezione, grazie alla quale è possibile estendere, talora con notevoli semplificazioni, risultati grafici e analitici a configurazioni “duali” di quelle considerate. Tipiche forme duali sono il fascio e la punteggiata (nel piano), la stella e il sistema piano (nello spazio).

Invarianti

Sono invarianti quelle proprietà che non variano con operazioni di proiezione e sezione, precisamente la collinearità (appartenenza di tre punti a una retta), dualmente l’incidenza (l’appartenenza di tre rette a un fascio), e il birapporto. Questo esprime in valore numerico adimensionale la relazione metrica fra quaterne di elementi in corrispondenza proiettiva, calcolata come rapporto dei rapporti delle distanze fra i punti delle rette (ABCD) o, dualmente, degli angoli fra le rette o fra i piani dei fasci (abcd), considerandone il verso. Di particolare rilievo è il birapporto armonico, dal valore numerico pari a -1.

Trasformazioni

Trasformazioni proiettive sono quelle basate su operazioni di proiezione/sezione, potendo essere propri e/o impropri gli elementi implicati nei procedimenti. Ponendo in relazione grafica e logica le configurazioni del piano e dello spazio, esse definiscono e verificano le proprietà, incluse le “invarianti”, sicché dicesi trasformazione proiettiva ogni trasformazione che conserva gli invarianti proiettivi. Trasformazioni notevoli della geometria proiettiva sono la prospettività, la proiettività, l’omologia, caratterizzate nel piano iconico da opportune omografie, ovvero da coppie o serie di immagini proiettivamente connesse, graficamente derivabili l’una dall’altra.

Prospettività

La prospettività è una relazione tra forme proiettive a elementi comuni coincidenti. Essa intercorre nel piano fra punteggiate e, dualmente, tra fasci; nello spazio, fra piani e, dualmente, fra stelle; o tra forme di terza specie. Elementi uniti coincidono nella trasformazione, elementi limite corrispondono a elementi impropri.
La proiettività è una corrispondenza proiettiva, a elementi comuni non coincidenti, fra due terne di elementi arbitrariamente assunti su due forme fondamentali distinte; un’equivalente definizione legata a importanti applicazioni la enuncia come corrispondenza che trasforma coniche in coniche. Essa si avvale di opportuni elementi di collineazione (asse per le rette, dualmente centro per i fasci), potendosi estendere alle forme di seconda e di terza specie. La definisce il “teorema fondamentale della proiettività”, ritenuto il più significativo della geometria proiettiva.
L’omologia è una corrispondenza tra forme proiettive su piani sovrapposti (omografia), originata nello spazio per proiezione di prospettività fra piani o, dualmente, per sezione di prospettività fra stelle. E’ la trasformazione più generale della geometria proiettiva Ne sono elementi notevoli il centro (dell’omologia), l‘asse (dell’omologia), le rette limite (omologhe delle rette improprie). Conserva gli invarianti e in particolare il birapporto, definito anche invariante assoluto o caratteristica dell’omologia. A seconda della natura (propria o impropria) e della posizione spaziale degli enti generatori si ottengono, accanto alla forma canonica, affinità, omotetie, simmetrie e traslazioni, nonché corrispondenze involutorie come la polarità. Ogni omologia può ricondursi a un’omologia di ribaltamento, con utili applicazioni nella ricerca della vera forma delle configurazioni rappresentate. In riferimento alle forme di terza specie si definisce infine l’omologia solida.

Configurazioni notevoli

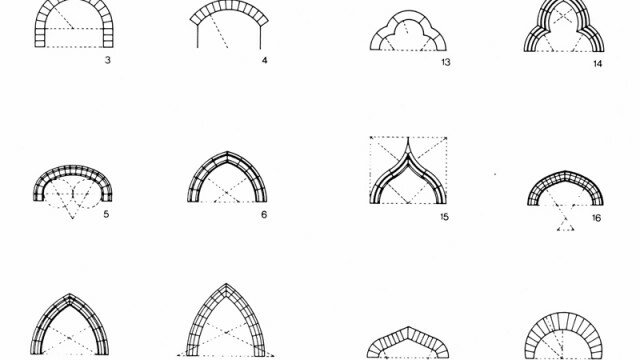
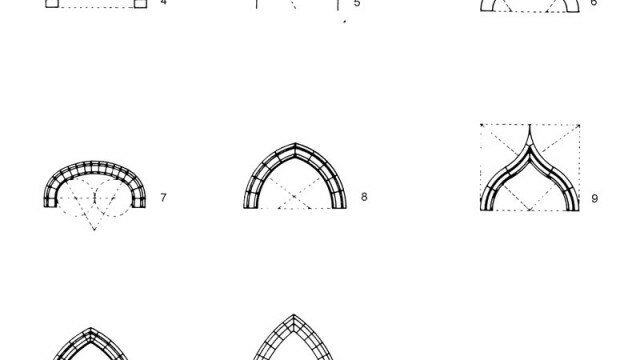
Fra le configurazioni notevoli della geometria proiettiva, il quadrilatero piano completo e, dualmente, il quadrangolo piano completo, esprimono graficamente il birapporto armonico, specie in relazione alle coniche (involuzione, polarità). Legate anche alle configurazioni duali del triangolo e del trilatero, dell’esalatero e dell’esagramma, e in generale ai multilateri e ai poligoni, le coniche rivestono un rilievo speciale in geometria proiettiva sia sul piano storico che scientifico. Banco di prova e sorgente di ricerche, applicazioni e scoperte, alla teoria delle coniche nel piano corrisponde la teoria delle superfici quadriche (superfici di secondo grado) e delle curve quartiche (curve di quarto grado) nello spazio. Lo studio delle configurazioni della geometria proiettiva si avvale oggi proficuamente della modellazione digitale.

Cenno storico

Formalizzata nel XIX secolo, la geometria proiettiva si basa su principi geometrici di origine remota. Anticipazioni della proiezione e sezione rimontano, con dovute cautele storiche, alle principali opere di Euclide (III a.C.), l’Ottica e gli elementi, mentre la sintesi come proiezione/sezione avviene molto più tardi con le sperimentazioni prospettiche di Brunelleschi (1377-1466), primi esempi di “trasformazioni proiettive” da cui prendono avvio la geometria descrittiva e la geometria proiettiva. Riferimenti indiretti ai temi della geometria proiettiva si ritrovano in vari campi del sapere, dall’arte all’architettura, dall’astronomia, alla fisica, alla matematica pura.
I fondamenti disciplinari sono posti da Girard Désargues (1591-1661), sia nei metodi che delle applicazioni. A lui si devono i concetti di spazio rigato e di spazio di piani, l’introduzione del punto e del fascio impropri, la rivoluzionaria concezione delle coniche come proiezioni/sezioni del cerchio, l’analogia proiettiva fra cono e cilindro e quindi fra proiezioni parallele e prospettiche. Altre deduzioni riguardano l’equivalenza proiettiva fra retta, cerchio e coniche degeneri, le proprietà involutorie delle coniche e la polarità, quest’ultima estesa al caso tridimensionale della sfera. Fra i caposaldi metodologici ricordiamo il teorema dei triangoli corrispondenti, che proposto nella duplice versione spaziale e piana definisce la prospettività fra piani e pone le basi dell’omologia. Le sue opere, basate su procedimenti grafici hanno tuttavia scarsa fortuna a causa del maggiore interesse suscitato dai procedimenti analitici promossi dal suo contemporaneo Descartes (1596-1640).
I suoi studi sono comunque ripresi e ampliati, in particolare da Blaise Pascal (1623-1662), noto per il teorema dell’esagramma inscritto in una conica, e da Philippe de La Hire (1640-1718), che approfondisce la polarità e studiò la configurazione spaziale degli elementi generatori dell’omologia, introducendovi l’impiego della retta limite.
La prima sistematizzazione della disciplina si ha con Jean Victor Poncelet (1788-1867) il quale conferisce alla materia la massima astrazione, stabilendone definitivamente il carattere grafico. Avvalendosi della proiezione centrale per lo studio delle proprietà metriche delle figure definisce le proprietà invarianti, compreso il birapporto, conferma la validità del principio di continuità per le trasformazioni proiettive, per questa via estendendo la nozione di ente improprio alla retta e al piano, e in relazione alla teoria delle coniche individua i punti ciclici, elementi immaginari del campo complesso. Altro importante contributo riguarda la codificazione dell’omologia piana e solida che preluse, mediante l’impiego della polarità nello studio delle superfici quadriche, alla successiva formulazione del principio di dualità, dovuta a Joseph-Diaz Gergonne (1771-1859).
L’assetto disciplinare definitivo si deve invece a Christian von Staudt (1798-1867), definito l’“Euclide del XIX Secolo”, cui va il merito di aver sintetizzato nel “teorema fondamentale della proiettività” la condizione necessaria e sufficiente di questa relazione. Grazie anche agli ulteriori approfondimenti sulla dualità, la proiettività, la definizione autopolare delle coniche, il ricorso agli elementi immaginari, l’adozione di un metodo assiomatico scevro da considerazioni metriche, egli contribusce a definire la geometria proiettiva come disciplina autonoma.
Seguono importanti perfezionamenti, fra cui il teorema di Jacob Steiner (1796-1863) sulla generazione proiettiva delle coniche per corrispondenza fra coppie di rette proiettive o, dualmente, di fasci proiettivi, a coronamento del lungo intreccio storico fra questa disciplina e gli studi sulle coniche.
Completano il ciclo le deduzioni di Ferdinand Möbius (1790-1868) sulla biunivocità delle trasformazioni, sulle omografie e sulle collineazioni. Non meno decisiva l’asserzione di Arthur Cayley (1821-1895) secondo cui tutte le proprietà metriche delle figure sono suscettibili di interpretazione proiettiva qualora riferite all’“assoluto” proiettivo (ovvero al sistema degli elementi impropri), con l’importante conseguenza che la stessa geometria metrica sarebbe una branca della proiettiva, coincidendo quest’ultima con l’“intera” geometria.
Di qui il rilievo che la geometria proiettiva assume nell’ambito della matematica moderna. Riconosciuta disciplina autonoma, in base alla teoria dei gruppi è definita da Felix Klein (1849-1925) come branca inerente al gruppo delle trasformazioni proiettive, particolarmente significativo restando tali trasformazioni valide anche negli iperspazi (spazi a più di tre dimensioni) e in campi non-euclidei (spazi curvi non basati sul postulato delle parallele). La geometria proiettiva è quindi parte attiva nelle moderne teorie dello spazio anche in relazione alle geometrie superiori e al decisivo passaggio dall’impostazione assiomatico-deduttiva, legata all’evidenza percettiva dei principi primi, all’approccio ipotetico-deduttivo basato invece sull’evidenza logica degli stessi. La geometria proiettiva fornisce inoltre alla Matematica metodi di costruzione e visualizzazione delle configurazioni, mentre alcune proprietà (polarità), approfondite da vari studiosi fra i quali Luigi Cremona (1830-1903) trovano importanti riscontri anche in fisica (statica grafica).
Con riferimento all’architettura, centrata sullo studio e la configurazione degli spazi, il valore essenziale della geometria proiettiva consiste nelle relazioni che essa istituisce fra immagine e realtà, sia sotto il profilo grafico (di prevalente matrice artistica, principiato con la prospectiva pingendi) che sotto il profilo metrico (di prevalente matrice scientifica, principiato con la prospectiva prattica), fondamentali per l’architettura e la sua rappresentazione, sia essa di rilievo o di progetto, laddove le valenze estetiche non sono indipendenti dal controllo metrico della forma.
Le due componenti risultano attualmente integrate nei dispositivi di modellazione digitale.

Bibliografia

Boyer C.B., Storia della Matematica. Prefazione di Lucio Lombardo Radice, Oscar Mondadori, Milano, 1980; Coxeter H.S.M., Projective Geometry. Second Edtion, University of Toronto Press, Toronto and Buffalo, 1974; De Rosa A., Sgrosso A., Giordano A., La Geometria nell’Immagine. Storia dei metodi di rappresentazione, Tomi I, II, III, UTET, Torino, 2000-2002; Enriques F., Lezioni di Geometria Proiettiva. Seconda edizione aumentata, Ditta Nicola Zanichelli, Bologna, 1904.

Copyright © - Riproduzione riservata